Uma preocupação permanente na estratégia Seis Sigma é a redução da quantidade de desperdício, que tecnicamente é denominada de “defeitos”. Na estratégia Seis Sigma, defeito é qualquer desvio de uma característica que gere insatisfação ao cliente (externo ou interno).
O fato de que um processo Seis Sigma equivale à redução de defeitos em produtos ou serviços para um nível de 3,4 defeitos por milhão causa um bloqueio inicial às instituições, que julgam ser praticamente impossível.
Todavia, mesmo grandes e famosas empresas que adotaram a estratégia Seis Sigma, como a GE e a Motorola, alcançaram esse nível em alguns de seus processos. A adoção da estratégia as direciona para busca permanente da melhoria nos demais processos.
Ressalte-se que uma empresa que utiliza máquinas sofisticadas, desenvolve processos inteiramente automatizados e fabrica produtos de altíssima precisão e sem defeitos não necessariamente representa uma organização Seis Sigma, se nessa empresa existirem outros processos ineficientes e pessoas descomprometidas. Uma instituição, porém, pode iniciar a estratégia Seis Sigma melhorando alguns processos e convivendo com outros que optar por manter sem alterações devido a limitações de recursos.
Ao adotar o Seis Sigma, uma instituição não precisa obrigatoriamente utilizar esse nome. Muitas instituições adotaram a estratégia Seis Sigma e a chamaram por nomes próprios. Porém, mais importante que o nome é o resultado alcançado.
- Fonte:
- Revista FAEBUSINESS , n.5, abr. 2003

doutorcep@datalyzer.com.br
Curvas normais, com qualquer μ e σ, podem ser transformadas em uma curva normal que tem média igual a 0 (μ = 0) e desvio padrão igual a 1 (σ = 1). Esta curva normal, com média 0 e desvio padrão 1, é conhecida como curva normal reduzida. Suas probabilidades são apresentadas em tabelas de fácil utilização.
Como a normal é simétrica, a tabela apresenta somente as probabilidades da metade direita da curva. A probabilidade de um intervalo qualquer da metade esquerda é igual à probabilidade do intervalo equivalente na metade direita.

Figura 1 - Tabela de probabilidades da curva normal reduzida
Como usar a tabela para obter as áreas ou probabilidade
A tabela anterior retorna a probabilidade de ocorrência de um evento entre 0 e z. Na margem esquerda há o valor de z com uma decimal e, se for necessário considerar a segunda decimal, deve-se procurá-la na margem superior. Observe a tabela abaixo, que destaca a probabilidade de ocorrer um valor entre 0 e 0,62.
Exemplos
- Para calcular a probabilidade de z entre 0 e 1, procuramos na margem esquerda a linha que tem z = 1,0 e a coluna 0,00, e encontramos o valor 0,3413. Isto significa que a probabilidade de encontrar um valor de x entre a média zero e z = 1,0 é 0,3413, ou 34,13%.
- Por outro lado, para se obter a probabilidade de z maior que 1, calculamos a probabilidade de z entre 0 e 1, que é 0,3413, e a seguir fazemos 0,5 - 0,3413 = 0,1587, ou 15,87%.
- Para se obter a probabilidade de z entre 0 e 1,87, procuramos a célula cuja linha é 1,8 e coluna 0,07. O resultado é o valor 0,4693 ou 46,93%.
Como transformar uma normal qualquer em uma normal reduzida
Para transformar uma curva normal em uma curva normal reduzida, devemos calcular o z equivalente aos limites desejados utilizando a fórmula:
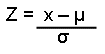
μ = média da normal original
σ = desvio padrão da normal original
Exemplo
Considerando que a idade de um grupo de 20 pessoas segue uma distribuição normal, e que a média de idade do grupo é de 60 anos e o desvio-padrão é igual a 4, calcule a probabilidade de uma pessoa possuir uma idade entre 60 e 69 anos.
O procedimento é simples. Precisamos saber qual é o intervalo da normal reduzida que é equivalente ao intervalo 60 a 69 da normal original. Aplicando a fórmula da curva normal reduzida, são calculados os valores de z para x=60 e x=69.
Para x=60

Para x=69
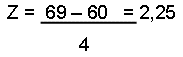
O ponto 60 corresponde a z = 0 e o ponto 69 a z = 2,25. Assim, o intervalo 60-69 da curva normal original é equivalente ao intervalo 0-2,25 da normal reduzida.
Como a probabilidade de z entre 0 e 2,25 é 0,4878 ou 48,78% (observe a tabela abaixo), podemos afirmar que a probabilidade de uma pessoa possuir idade entre 60 e 69 anos é igual a 0,4878 ou 48,78%.

Figura 3 - Tabela de probabilidades destacando a ocorrência do valor 2,25 em uma curva normal reduzida
Por outro lado, a probabilidade de idades maiores que 69 é igual à probabilidade de z maior que 2,25, que é igual a 0,5 – 0,4878 = 0,0122 ou 1,22%.
A probabilidade de existirem pessoas com idade menor que 60 é 0,50 ou 50%, pois 60 equivale a z igual a 0 e, seguindo o conceito da curva normal reduzida, a probabilidade de z < 0 é 0,50.
Para dados distribuídos em uma curva normal, um caminho simples e rápido para conhecer a probabilidade de ocorrência de um evento é utilizar a curva normal reduzida.
Até a próxima edição, pessoal!