

A qualidade é relativa. O que é qualidade para uma pessoa pode ser falta de qualidade para outra.
"G. Weinberg"
O conceito de qualidade é aparentemente intuitivo levando as pessoas a considerá-la como “satisfação”, “melhor”, “confortável”, “seguro”, etc.
Vamos ver um exemplo prático:
Imagine que se deseja adquirir uma camisa para uma ocasião importante. Se o preço do produto é muito além das expectativas, este se torna um impedimento para a compra. Então o preço inconveniente passa a ser encarado como um defeito!
Se o tamanho não está disponível no estoque, a disponibilidade do produto é também um fator de QUALIDADE e sua ausência implica em mais um defeito.
Mas, supondo que tudo anteriormente apresentado estivesse em conformidade com as expectativas, a camisa poderia apresentar algum problema como a falta de manga, de cor, de botão, de costura, de maciez no tecido..., e outras faltas, ou seja, se ela tem algum defeito de fabricação. Caso tenha alguma anormalidade, a compra não seria efetuada, pois não foram atendidas as expectativas. O que se procura então numa camisa para uma ocasião importante? QUALIDADE ou defeitos?
Nesse caso, se a decisão pela compra é feita quando não se encontra defeitos, logo se pode admitir que a camisa possui QUALIDADE! O conceito de qualidade pode então ser definido como “Ausência de defeitos”.
Entretanto quando examinado mais longamente, o conceito revela-se complexo. Definir um conceito de qualidade para estabelecer objetivos é, assim, uma tarefa menos trivial do que aparenta a princípio.
Supondo que se esteja diante de produtos alternativos, como escolher o melhor? Esse problema de julgamento acontece com qualquer pessoa cotidianamente, quando se consomem itens como roupas, música, comida ou filmes. Mas curiosamente, apesar da freqüência com que avaliamos os objetos à nossa volta, é muito difícil obter consenso a respeito da qualidade de um produto. Isso se traduz, por exemplo, no fato de existir uma profusão de marcas de eletrodomésticos e haver clientes felizes adquirindo aparelhos de marcas diferentes.
Uma escolha torna-se mais clara quando se estabelecem critérios que sirvam para julgar um produto. Em algumas situações, tais critérios são relativamente simples de identificar e estabelecer. Por exemplo: em domínios como engenharia elétrica ou mecânica, as informações necessárias são obtidas em função da finalidade a que se destina um determinado produto. Para dispositivos simples, como um fusível ou uma engrenagem, não é difícil enumerar algumas características que provavelmente são relevantes: ponto de fusão, condutância térmica, resistência a cisalhamento ou dimensões físicas.
Isto nos leva à famosa definição de Crosby [1992]: "A qualidade é conformidade aos requisitos". Essa definição é interessante, pois deixa explícito o fato de que é preciso um ponto de referência para julgar um produto. Traz embutida a idéia de como efetuar esse julgamento e, por fim, mostra como o processo todo pode ser documentado, analisado e os resultados transmitidos a outras pessoas.

doutorcep@datalyzer.com.br
Finalizando nossa série sobre os índices estatísticos, falaremos neste mês sobre os Índices de Performance Pp e Ppk.
Os índices de Capacidade informam como o processo poderá agir no futuro, já os índices de performance informam como o processo agiu no passado ou está agindo no momento.
O cálculo dos índices de performance é muito semelhante ao dos índices de capacidade, salvo o que diz respeito ao desvio-padrão utilizado.
Até 1991, essa pergunta não tinha uma resposta exata. Para eliminar essa confusão, a ASQC - American Society for Quality Control (Sociedade Americana de Controle da Qualidade) publicou naquele ano "o manual fundamental de referência do Controle Estatístico de Processo".
O que está definido no manual publicado pela ASQC é que os índices de capacidade do processo utilizam o desvio-padrão estimado e os índices de performance utilizam o desvio-padrão calculado sobre os valores individuais do processo.
Você perceberá, em seguida, que o cálculo dos índices de Performance do processo é idêntico ao cálculo dos índices de Capacidade, exceto que o desvio-padrão utilizado é o calculado.
Vamos rever os cálculos...
Os índices de Performance do processo utilizam o desvio-padrão calculado.
Considerando os dados utilizados no informativo do mês de agosto de 2006
clique aqui para acessaá-lo),
temos:
LSE (Limite Superior de Especificação) = 2.5
LIE (Limite Inferior de Especificação) = 0.05
 (Desvio-padrão calculado) = 0.5350
(Desvio-padrão calculado) = 0.5350
A fórmula do índice Pp é dada por: ![]()
Na fórmula, percebemos , como foi escrito anteriormente, que este índice desconsidera a média do processo, retratando apenas sua variação.
O cálculo deste índice em nosso exemplo é dado por:
![]()
Os índices de Performance do processo utilizam o Desvio-padrão calculado (clique aqui para aprender a calculá-lo).
Considerando os dados utilizados no informativo do mês de agosto de 2006 (clique aqui para acessá-lo), temos:
LSE (Limite Superior de Especificação) = 2.5
LIE (Limite Inferior de Especificação) = 0.05
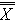 Média do processo (Média do processo) = 1.025
Média do processo (Média do processo) = 1.025
 (Desvio-padrão calculado) = 0.5350
(Desvio-padrão calculado) = 0.5350
A fórmula do índice Ppk é dada por: 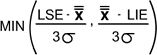
O cálculo deste índice em nosso exemplo é dado por:

Obs.: Atente-se para a simbologia do desvio-padrão. O desvio-padrão estimado é simbolizado por 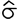 ,
já o calculado é simbolizado por
,
já o calculado é simbolizado por  .
.
Agora que já vimos como calcular os índices, vamos ver em gráficos quais os seus significados.
Sabemos que quanto mais estreita a curva da distribuição, menor a variação e maiores os valores dos índices Pp e Ppk. Sabemos ainda que quanto maior o valor de Pp e Ppk, melhor é o status do processo.
Considerando essa afirmação, vamos entender em quais ocasiões temos valores altos e baixos para esses dois índices.
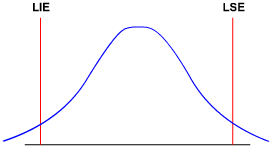
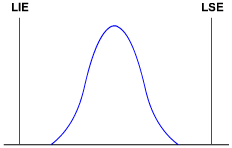
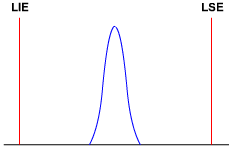
Nos três exemplos anteriores, os índices Pp e Ppk receberam os mesmos conceitos, mas nem sempre isso ocorre.
Veja no próximo exemplo em que há um processo com uma variação bem pequena, que gera um Pp ótimo e também geraria um Ppk com valor alto, mas a distribuição não está centrada entre os limites de especificação.
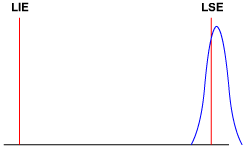
Como já vimos no mês passado, um processo, para ser capaz, necessita de centralização entre os limites de especificação e baixa variação.
Resumindo a utilização dos índices de Capacidade e Performance do Processo, temos:
| Índice | Uso | Definição |
| Cp, Pp | O processo está centrado entre os limites de especificação | Taxa de tolerância (a largura dos limites de especificação) à variação atual (tolerância do processo) |
| Cpk, Ppk | O processo não está centrado entre os limites de especificação, mas cai sobre ou entre eles | Taxa de tolerância (a largura dos limites de especificação) à variação atual, considerando a média do processo relativa ao ponto médio das especificações. |
Fonte: